LOVE ♡ LIVE 2024 *Honey bunny* でHoney Moonを聴くには。神奈川県民ホールの場合。

セトリのネタバレをします。

　

　

今回のツアーでは世界観映像と言うのか、モチーフ映像と言うのか、抽象的な映像が無い事に加えてセトリの変化が不規則過ぎるのであまりセトリのネタバレで怒られそうにない雰囲気を勝手に感じています。

なので普段なら躊躇うセトリ予想を公開ブログでしてみます。

ちなみに８公演目の京都が終わった時点でのセトリ集は下記のような感じです。

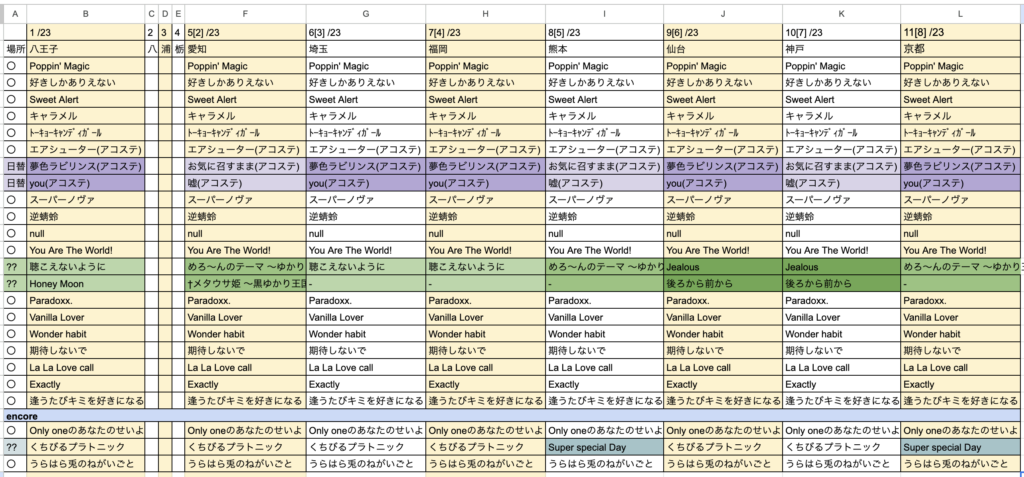
紫の行はパターンはわからないのですが、曲としては一応２タイプ。[夢色&you or お気に&嘘]

問題は緑の行で、よく分からない。

加えてアンコール２曲目もSuper special Dayという新規(?)を置いていくスタイルの凄い選曲。

　

8公演やって今回のように自由なセトリ変化があるのは恐らく初めてなのでランダムでしょと思っています。

でも、純粋に次の曲が来る確率を考えながら聴くと聴きたい曲に当たった時の感動が増幅されると思うので以下ではあえて予想をしていきたいと思います。

先ずは妄想ベースで考えると、下記のような要素で意見が割れると思います。

• 休止ライブでセトリがズレた or 公演Noでセトリが決まっている
• 曲のタイトルに対してセトリの番号が動くことはない[例：国家とメタウサの曲順反転]
• 23曲歌う日と24曲歌う日で、喉の負荷を調整している［ドクターストップ］
• 次の日のスケジュールによる[宿泊 or 日帰り]
• ツアー前半後半で日替わりセトリを変えそうな気がする

上記の妄想条件を潜り抜けてHoney Moonが確率的に安全に聴けるのはツアー前半と見做せる神奈川、高崎、水戸なんじゃないの？と感覚的に思っています。(ツアー後半は何が起こるのか分からないので。。。)

何でHoney Moonの聴ける確率を考えているのか？についてですが、ツアータイトルがHoney bunneyだからです。

他に理由はありません😤

忙しい人向けに結論を先に言うと、好きな曲を聴きたかったらまずはチケットを買え。[ローチケlink]

　

ちょっと結論が下品だったので口直しにベイズ推定を使ってセトリの遷移確率を考えたいと思います。

曲名を直書きするのは大変なので一旦アルファベットに直します。

alphabet	曲名
A	夢色ラビリンス
B	お気に召すまま
C	聴こえないように
D	国家(めろ〜んのテーマ)
E	Jealous
F	Honey　Moon
G	メタうさ姫
H	無し(23曲バージョンのセトリ)
I	後ろから前から
J	くちびるプラトニック
K	Super special Day

• Aの「夢色ラビリンス」とBの「お気に召すまま」は次の曲が今のところ確定なので、嘘とyouを省いて考えています。
• Hは歌っていない場合で、23曲の場合です。

このアルファベットを使っていわゆる事前分布を書いてみました。

# 遷移確率 [セトリ変更曲数]
1曲目:  'A': 5/8, 'B': 3/8,
2曲目:  'A': {'C': 3/5, 'D': 1/5, 'E': 1/5},
        'B': {'D': 2/3, 'E': 1/3}
3曲目:  'C': {'F': 1/3, 'H': 2/3},
        'D': {'G': 1/2, 'H': 1/2},
        'E': {'I': 1}
4曲目:  'F': {'J': 1},
        'G': {'J': 1},
        'H': {'J': 3/4, 'K': 1/4},
        'I': {'J': 1}

この遷移確率に従うのであれば、次の公演は1曲目が5/8(63%ぐらい)で「夢色ラビリンス」が歌われるハズで、Honey Moonは12.5%ぐらいの確率で神奈川で歌われるハズです。

P(A) = 5/8
P(C|A) = 3/5
P(F|C) = 1/3

P(F|A and C) = (5/8) * (3/5) * (1/3) = 0.125

ところが、この方法で計算してしまうと「お気に召すまま」が歌われたときにHoney Moonの可能性が0になり絶望してしまう場合がありますのでもう少し希望の多い確率モデルを考えました。
(仙台・神戸では最初の曲を無視してJealous固定だったんだからきっと希望はあるはずです。)

語弊があるかと思いますが尤度をぼかせばいいので下記のようなコードで計算してみました。

import itertools

# 既存のセットリストデータ
existing_setlists = [
    ['A', 'C', 'F', 'J'],
    ['B', 'D', 'G', 'J'],
    ['A', 'C', 'H', 'J'],
    ['A', 'C', 'H', 'J'],
    ['B', 'D', 'H', 'K'],
    ['A', 'E', 'I', 'J'],
    ['B', 'E', 'I', 'J'],
    ['A', 'D', 'H', 'K']
]

# 選ばれうる曲
choices = {
    1: ['A', 'B'],
    2: ['C', 'D', 'E'],
    3: ['F', 'G', 'H', 'I'],
    4: ['J', 'K']
}

# 事前確率の計算
def prior_probability(song, position):
    count = sum(1 for setlist in existing_setlists if setlist[position - 1] == song)
    return count / len(existing_setlists)

# ラプラススムージングを用いた尤度の計算
def likelihood(song, position, conditions):
    alpha = 1  # スムージングパラメータ
    count = sum(1 for setlist in existing_setlists 
                if all(setlist[pos - 1] == cond for pos, cond in conditions.items()) and setlist[position - 1] == song)
    total = sum(1 for setlist in existing_setlists 
                if all(setlist[pos - 1] == cond for pos, cond in conditions.items()))
    # ラプラススムージング適用
    return (count + alpha) / (total + alpha * len(choices[position]))

# 条件付き確率の計算（ベイズの定理）
def bayes_theorem(prior, likelihood, marginal):
    return (likelihood * prior) / marginal if marginal > 0 else 0

# 曲Fが歌われる確率
def probability_of_song_F(conditions):
    prior_F = prior_probability('F', 3)
    likelihood_F = likelihood('F', 3, conditions)
    marginal_F = sum(likelihood(song, 3, conditions) * prior_probability(song, 3) for song in choices[3])
    return bayes_theorem(prior_F, likelihood_F, marginal_F)

# 曲B,Dが選択された場合の曲Fの確率
conditions = {1: 'A', 2: 'C'}
prob_F_given_BD = probability_of_song_F(conditions) * 100
print(f"曲A, Cが選択された場合の曲Fの確率: {prob_F_given_BD:.2f}%")

# 可能なセットリストの生成
def generate_possible_setlists(conditions):
    possible_setlists = []
    for combination in itertools.product(*choices.values()):
        if all(combination[pos - 1] == cond for pos, cond in conditions.items()):
            possible_setlists.append(combination)
    return possible_setlists

possible_setlists = generate_possible_setlists(conditions)
print("可能なセットリスト:")
for setlist in possible_setlists:
    print(setlist)

上記のコードで三連単を推論させてみると下記の感じ。

• 夢色ラビリンス　->　聴こえないように　->　Honey Moon : 11.8%
• 夢色ラビリンス　->　国家(めろ〜んのテーマ)　->　Honey Moon : 8.3%

• お気に召すまま　->　聴こえないように　->　Honey Moon : 12.5%
• お気に召すまま　->　国家(めろ〜んのテーマ)　->　Honey Moon : 7.7%

　

神奈川でも「Jealous」みたいな曲が突然ぶっこまれる可能性が無くもないような気はしますが、通常運転であれば「聞こえないように」or国家は硬いんじゃないかと思います。
(本音を言うと流れ星ジェニーとかビバルディみたいなのが来そうな気がしますが。)

そのうえでHoney Moonが聴きたい人は座席を丁寧に使いながら１割を信じて祈りましょう。

まとめると、本当にゆかりさんの古い曲を聴きたい古のヲタクが居たらもう本当に最後のチャンスかもしれないのでチケットを買ってみてください！！きっとワンチャンあります！！！